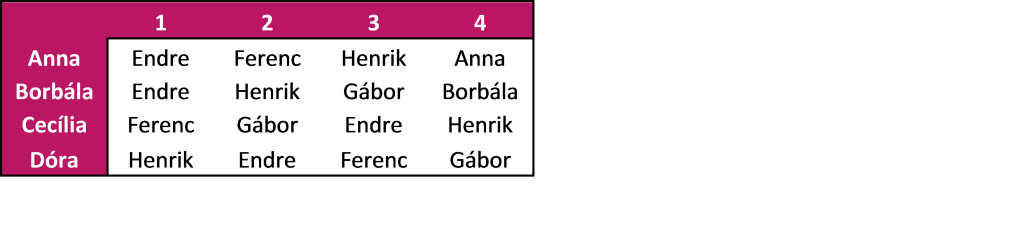2016.07.26-án derültek ki a felsőoktatásba bekerüléshez szükséges érettségi ponthatárok, amelyek több ezer magyar fiatal jövőjét határozzák meg. Felmerülhet a kérdés: honnan is tudja az Oktatási Hivatal, hogy hol kell meghúzni a határt?

A válasz elsőre egyszerűnek tűnhet: minden szakra van egy létszámkorlát, az utolsó bekerülő pontszáma a felvételi ponthatár. Ez azonban egy másik, sokkal fundamentálisabb kérdéshez vezet: hogyan dől el, hogy kik járhatnak az adott szakra?

A fenti, kiemelt kérdésre a közgazdaságtan, azon belül a játékelméletnek nevezett terület adhat választ. A játékelméletnek kevés köze van a „játék” szó köznapi értelméhez. A játékelmélet célja, hogy olyan döntési szituációkat vizsgáljon, ahol az egyéni szereplők jóléte, „kifizetése” nem csak a saját döntésétől függ, hanem mások döntéseitől is.

Egy tipikus játékelméleti probléma a Potyautas probléma, aminek a legtipikusabb példája az egyetemi előadások hallgatása. Ha mindenki bemegy az órára, a tanár elégedett lesz, azonban ez a hallgatók számára egyénenként költséggel jár. Ha nem mennek be az órára, időt és energiát spórolhatnak, azonban a tanár nem fog örülni. Ebben a szituációban a végkifejlet, hogy elégedett lesz-e a tanár a hallgatókkal, az egyszeri hallgató számára nem csupán a saját döntésétől függ, hanem a többiekétől is. A játékelméletnek azon területét, ami a párosítási mechanizmusokkal – mint amilyen az egyetemekr bekerülő diákok meghatározása – foglalkozik, matching-elméletnek nevezik. Egy tipikus párosítási probléma a Stabil Házasság Probléma.

Stabil Házasság Probléma

Tegyük fel, hogy a mi feladatunk egy kis faluban párválasztást szervezni az eladósorban lévő négy leány (Anna, Borbála, Cecília, Dóra), és négy fiú (Endre, Ferenc, Gábor, Henrik) kérő között. Mind a fiúk, mind a lányok preferenciái (kinek ki mennyire tetszik) ismertek, és a következő táblázatban találhatóak meg. A táblázatból kiderül, hogy Gábornak Borbála tetszik a legjobban, Dóra pedig a legkevésbé. Érdemes megjegyezni, hogy Henrik esetében ha Henrik sem Annát, sem Borbálát nem veheti feleségül, akkor inkább marad agglegény (saját magát választja párnak).

A célunk kettős: egyrészt azt szeretnénk, ha ez a párosítás stabil lenne.

Tegyük fel, hogy Anna – Endre és Borbála – Ferenc párok születtek a párosításunk során. Azonban Endre szívesebben házasodna Borbálával, mint Annával, és Borbála is szívesebben házasodna Endrével, mint Ferenccel. Így Endre és Borbála megszöknek egy távoli országba egymással. Ha létezik ilyen pár akik szivesebben lennének együtt annál mint amit a párosítás beosztott nekik, a párosítás nem stabil.

A jó hír, hogy a Házasság Problémának van megoldása, egy algoritmus („Deferred-Acceptance Algorithm”), amit David Gale és Lloyd Shapley publikált 1962-ben. Az elképzelést 2012-ben Nobel – díjjal jutalmazták.

Az algoritmus meglehetősen egyszerű:

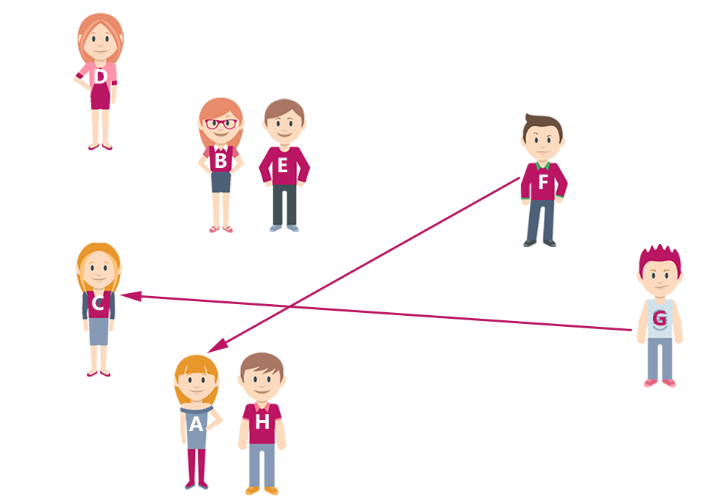
1. lépés: Minden fiú elmegy lánykérőbe ahhoz a lányhoz, aki a legjobban tetszik neki. Minden lány azt választja a kérői közül, aki neki a legjobban tetszik.
2. lépés: Azok a fiúk, akiknek nem jutott pár az első körben, elmennek lánykérőbe a második preferenciájukhoz. Ebben az esetben is minden lány azt választja, aki a legjobban tetszik neki a kérői közül. Akkor is, ha az előző körben már talált párt. Azaz az eljegyzések felbonthatóak.

Ez a folyamat addig ismétlődik, amíg van olyan fiú akit visszautasítottak.

A fenti példában az algoritmus két körben lezárul, Bori és Endre, Anna és Ferenc illetve Cecília és Gábor alkotnak párokat, Henrik agglegény, Dóra pedig vénlány marad.

                   

 1. kör

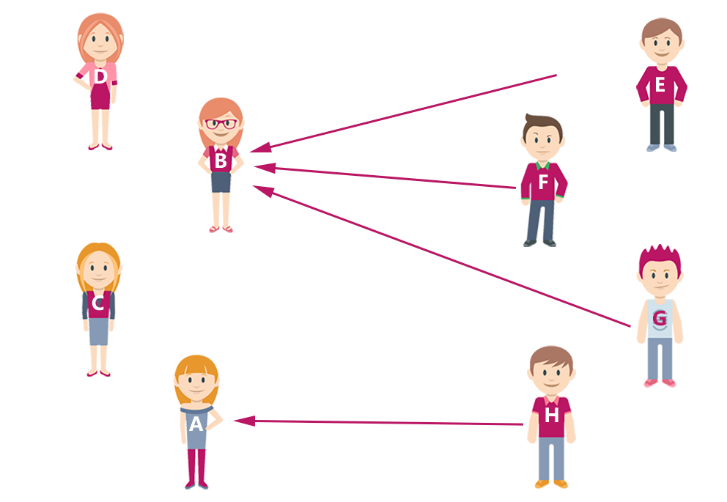
 2. kör

Végeredmény

Az algoritmus bizonyíthatóan mindig stabil párosítást eredményez. Azonban van egy kisebb bökkenő: a preferenciák alapján legtöbbször több stabil megoldás is elképzelhető.

Az fent leírt mechanizmus a fiúkat részesíti előnyben, egész egyszerűen azért, mert a fiúk az összes lány közül választhatnak, míg a lányok csak a kérőik közül. A játékelmélet nyelvén szólva azt mondanánk: a mechanizmus Fiú-optimális. Ha legényvásár helyett leányvásárt tartanánk, más megoldást kapnánk, ami a lányoknak kedvez.

Érdemes megjegyezni, hogy amennyiben legényvásárt tartunk (azaz a rendszer a fiúknak kedvez), a lányoknak megéri hazudni a preferenciáikról. Matematikai úton bebizonyítható, hogy nem létezik olyan stabil párosítási mechanizmus, ahol senkinek nem éri meg hazudni. Ez az eredmény Alvin Roth nevéhez köthető, aki a mechanizmustervezés és játékelmélet terén végzett munkájáért a fent említett Shapley-vel megosztva kapta meg a 2012-es Nobel-díjat.

Az Egyetemi Felvételi Probléma

Roth munkássága – ahogy azt a blogon korábban is láthattuk – sok más mechanizmustervezési problémára is kiterjed, ilyen például az egyetemi felvételi kérdése is. Az Egyetemi Felvételi Probléma a Stabil Házasság Probléma egy általánosítása. Itt is két külön halmaz elemeit (egyetemek és hallgatók, fiúk és lányok helyett) kell párosítanunk, azonban ebben az esetben egy egyetemhez több hallgató fog kerülni. A problémát másképpen Kórház-Rezidens problémának is nevezik, ugyanis ez volt az egyik legelső alkalmazása az effajta párosítási mechanizmusnak.

A megoldási algoritmusa hasonló a házassági problémához, azonban még egy adatra szüksége van: az egyes szakok kapacitására. A cél is ugyanaz: egy stabil párosítást létrehozni, ami hallgató-optimális. Az egyetemek preferenciáit a felvételi pontszámok alapján tudhatjuk meg, míg a hallgatók preferenciáit a jelentkezésnél fejezhetik ki. Az algoritmus a következő:

1. lépés: Minden jelentkezőt besorolunk az első helyen megjelölt szakra. Azokon a szakokon ahova több diák van besorolva mint amekkora a kapacitás, a túlcsordulást okozó alacsony pontszámú diákok besorolását visszavonjuk.
2. lépés: Akik nincsenek besorolva sehova, azokat besoroljuk a második megjelölt helyre. Ezután újra visszavonjuk a túlcsordulást okozó diákok besorolását a pontszámaik alapján, függetlenül attól, hogy melyik lépésben soroltuk be őket.

És ez a folyamat addig ismétlődik, amíg mindenkit sikerül besorolni valahova, illetve akit nem, annak elfogynak a megjelölt helyei. A házasság problémához hasonlóan ez a párosítás is stabil lesz, és mivel a hallgatók mennek „leánykérőbe”, így a kapott megoldás a jelentkező hallgatók számára lesz optimális. Annyival még bonyolódik a folyamat, hogy amennyiben a végső párosításban van olyan szak, ahova kevesebb diák van besorolva mint a minimum amivel a szak elindulhat, ezt a szakot bezárjuk és a szak nélkül az egész folyamatot az elejéről kezdjük.

Amint kiderült, hogy ki melyik szakra jár, a legutolsó bejutó pontszáma lesz a felvételi ponthatár.

A bejegyzés megjelenésének apropója, hogy 2016-ban a Rajk László Szakkollégium diákjai Alvin Roth-nak adományozzák oda a Neumann János-díjat. A professzor szeptember elején érkezik Budapestre a díjátadásra, aminek során egy nyilvános előadást is tart majd. Az előadásra történő regisztráció és az esemény részletei hamarosan elérhetőek lesznek.

Illusztrációk: Bíró János