Matthew Jackson, akinek a Rajk László Szakkollégium tagjai 2015-ben odaítélték a Neumann-díjat, a hálózatkutatásban alkotott kiemelkedőt. A hálózatelmélet komplex hálózatok elemzéséhez nyújt széles körben alkalmazható, univerzális eszköztárat, Jackson például tanulmányozta hálózatelméleti módszerekkel a reneszánsz Itáliában kötött érdekházasságokat, munkaerőpiaci információkat közvetítő hálózatokat és középiskolai szerelmi viszonyokat is.

Könyvének egyik bevezető példája egy amerikai középiskola diákjai között végzett felmérésen alapul, ahol a megkérdezettek arra a kérdésre válaszoltak, hogy melyik más diákokkal közösültek korábban. A felmérés eredményeit az ábrán láthatjuk:

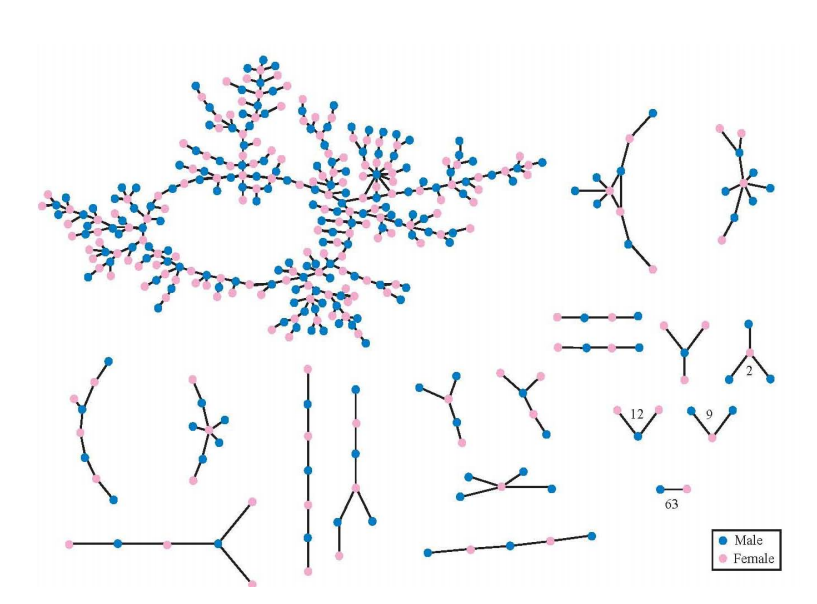
Ha két diák között volr szexuális kapcsolat, akkor össze vannak kötve. Az első dolog, amit észrevehetünk, az, hogy a hálózat csúcsait két csoportba sorolhatjuk: fiúk és lányok. Eszerint a fiúk általában lányokkal létesítenek kapcsolatot, míg a lányok fiúkkal (persze akadnak kivételek). Ezt a tulajdonságot a hálózatkutatók heterofíliának nevezik. Ez tágabb értelemben azt jelenti, hogy az egymásra valamilyen szempontból hasonlító csúcsok alacsony gyakorisággal létesítenek egymással kapcsolatot. Ennek ellentéte a homofília, amikor a hasonló csúcsok hasonló csúcsokkal létesítenek kapcsolatot. Ennek tipikus példája egy középiskola barátságainak hálózata.

Már megint Euler

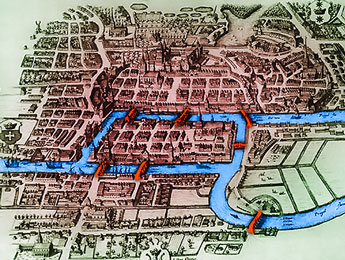
A hálózatkutatás tudománya egy relatíve fiatal társadalomtudományi kutatási terület, azonban alapjai jóval korábbra nyúlnak vissza: a gráfelméletre. A gráfelmélet kérdései a számítógépek megjelenése előtt elsősorban a gráfok tulajdonságai körül csoportosultak. Az egyik leghíresebb gráfelméleti kérdés a königsbergi hidak problémája, amelyet Leonard Euler oldott meg 1736-ban.

Königsberg négy városrésze Euler idejében hét híddal volt összekötve. A königsbergi hidak problémája azt a kérdést feszegeti, hogy át lehet-e menni Königsberg összes hídján úgy, hogy minden hídon csak egyszer haladunk át. (Ennek a problémának általános változata, hogy lehet-e úgy házikót vagy pálcikaembert rajzolni, hogy közben nem emeljük fel a ceruzánkat.)

A probléma megoldása egyszerű: Minden egyes szigetre (hálózatkutatásban:csúcsok) elmegyünk egy hídon (élek), és elhagyjuk azt egy másik hídon (kivéve persze azokat a szigeteket, amelyikről indultunk és végzünk). Tehát akkor létezik az Euler által keresett séta, ha 2 csúcs kivételével az összes csúcs fokszáma (azaz hogy hány él megy át rajta) páros szám. A kezdő csúcsnak és az utolsó csúcsnak lehet páratlan a fokszáma. Königsbergben azonban négy szigetből háromnak három a fokszáma, egynek pedig öt. Így ezeken szigeteket lehetetlen úgy bejárni, hogy az összes hídon átkelünk, azonban mindegyiken csak egyszer. (A pálcikaemberek megrajzolhatóságának problémáját az olvasóra bízom.)

Ahogy a számítástechnika fejlődött, lehetőség nyílt az analitikus módszerek mellett számítógépekkel vizsgálni egyre nagyobb hálózatokat, illetve ezekről empirikus adatokat gyűjteni. Így kezdődött el a társadalmi jelenségek hálózatkutatási vizsgálata.

A hálózat és a gráf fogalma nem elkülöníthető, hálózat fogalma alatt lényegében nagy gráfokat értünk. Hálózat például az, hogy ki kinek ismerőse Facebookon, hogy ki kinek a rokona, de hálózatot alkotnak a tudósok között a közösen írt publikációk is.

Vagy éppen az, hogy ki kivel élt nemi életet. A közgazdaságtan szexi.

Középiskolai kapcsolatok hálózata

Visszatérve gimis példánkra, a következő tulajdonság, amit megfigyelhetünk, hogy a hálózatnak van egy nagy, összefüggő része, az óriáskomponens, és sok kis, töredezett része. Ez két szempontból érdekes: egyrészt információval szolgál arról, hogy hogyan alakulhatott ki a hálózat, másrészt megkönnyíti annak vizsgálatát, hogy miként terjednek a nemi betegségek ezen a hálózaton.

Ez a hálózat tipikus esete az Erdős-Rényi-gráfnak (lásd a keretes írást), azaz a kapcsolatok véletlenül alakulnak ki a csúcsok között, minden fiú-lány kapcsolatnak nagyjából hasonló a valószínűsége. Ennek az ellentéte az lehetne, ha lennének rendkívül sok kapcsolattal rendelkező (nagy fokszámú) csúcsok, például ha lenne egy ellenállhatatlan fiú vagy lány az iskolában, aki mindenkivel összeszűri a levet.

Egy másik érdekes megfigyelés lehet az, hogy rendkívül kevés kör van a gráfban, és ami van, az általában nagy méretű (sok csúcsból áll). Ha egy csúcsból kiindulva bolyongunk a hálózaton, előbb-utóbb zsákutcába ütközünk, a csúcsok, amelyekkel az út során találkozunk, általában újak- tehát még nem találkoztunk velük. Ez rávilágít egy érdekes jelenségre azzal kapcsolatban, hogy hogyan veszítik el a szüzességüket a tinédzserek, illetve hogyan csatlakoznak a szexuális kapcsolatok hálózatához.

Ennyit erről a példáról, a többi érdekesség felfedezését ezután az olvasóra hagynánk.

Hálózattudományi cikksorozatunk folytatódik!

Matthew Jackson 2015 november 26-án tart előadást az ELTE ÁJK Dísztermében. Regisztráció hamarosan.