A cikk inspirációját Jordan Ellenberg “Hogy ne tévedjünk” c. könyvének előszava adta

A mindennapi életünkben sokkal többször találkozunk statisztikai, és valószínűségszámítási kérdésekkel, mint gondolnánk. Ami még inkább meglepő, hogy valószínűleg elég sokszor ítéljük meg tévesen ezeket a kérdéseket. A közgazdaságtan gyakorlása során is gyakran használt módszerek pedig bármely élethelyzetben segíthetnek, hogy helyesen döntsünk.

Kezdjük egy bonyolult problémával. Képzeljük el, hogy statisztikusok vagyunk a II. Világháború idején, és azzal bíznak meg minket, hogy állapítsuk meg a páncélzat optimális vastagságát a vadászgépeken. Bár ritkán gondolunk hősként a tudósokra, de eredményeik nagyban meghatározhatják egy háború kimenetelét.

A technológia fejlődésével egyre fontosabbá vált a hadviselésben is a rendelkezésre álló erőforrások mennyisége, illetve azok hatékony felhasználása. A modern háborút végső soron az nyeri, aki több erőforrással rendelkezik, vagy azokat hatékonyabban használja fel. A repülőgép páncélzata nehézzé teszi a gépet, ami miatt megnő a fogyasztása (és romlik a manőverezőképessége is). Tehát egy feleslegesen vastag borítás könnyen a háború megnyerésébe kerülhet kiegyenlített erőviszonyok mellett, hiszen az ellenségünk hatékonyabban használja az üzemanyagkészleteit. A túl üzemanyagtakarékos páncélzat pedig amellett, hogy a pilotákat is veszélynek teszi ki a drága repülőgépek árán keresztül bőven túltesz a megspórolt üzemanyagon. De hogyan is gondolkodjunk?

Nézzünk meg ehhez egy másik egyszerűbb példát. Sajnálatos módon egy nagyon pontos teszt (amely 99%-ban nem hibázik) azt az eredményt hozza, hogy súlyos betegségben szenvedünk. Mennyi a valószínűsége, hogy tényleg betegek vagyunk? A válasz sajnos (szerencsére!) nem a kézenfekvő 99%. Az esélyünk, hogy a teszt tévedett nagyban függ attól, hogy a betegség mennyire gyakori a teljes népesség körében. Például, ha a betegség a népesség 2%-át érinti, akkor az esélyünk arra, hogy tényleg betegek vagyunk valamivel kevesebb, mint 67%, ami felüdülést okozhat a 99%-hoz képest. Ha nem hiszi, járjon utána.

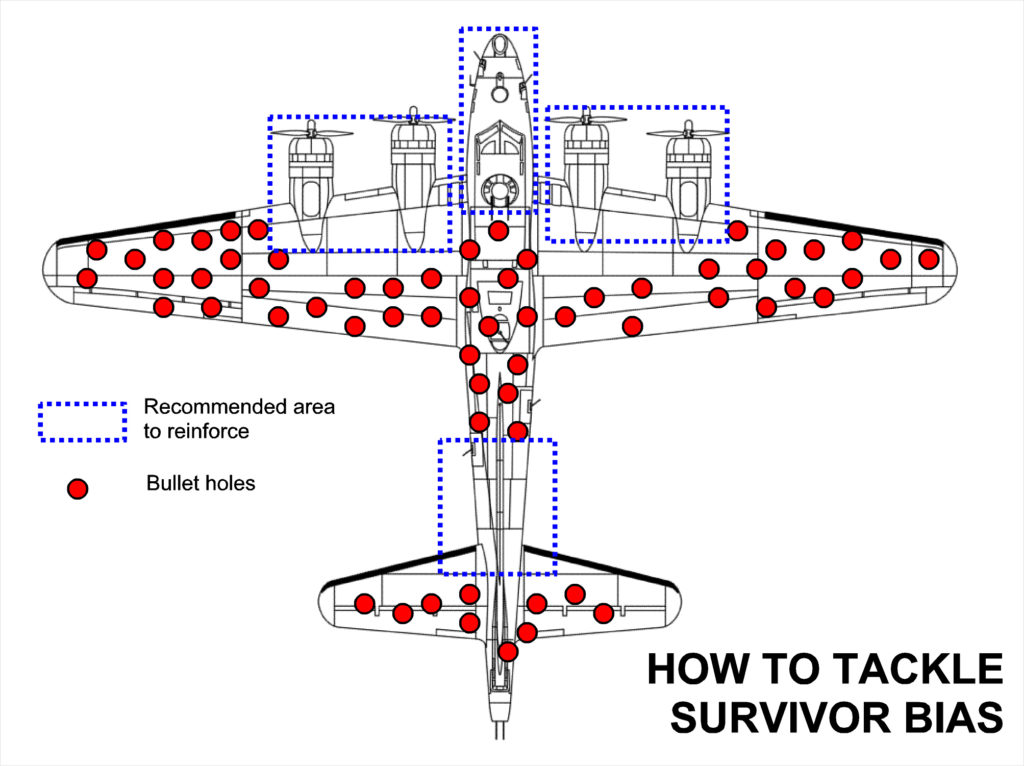
Na de hogy jön ez a repülők páncélzatához? Lássuk ehhez Wald Ábrahám hogyan oldotta meg a problémát. Az USA-ba emigrált magyar származású matematikus a bevetésről visszatérő gépeken található golyó ütötte lyukak eloszlását vizsgálta a repülőgépeken. Azt figyelte meg, hogy bizonyos helyeken sokkal több lyuk található, mint máshol. A repülőgép törzsén átlagosan jóval több golyónyomot számlált, mint a hajtómű, vagy az üzemanyagtartály környékén. Mire következtetnénk ebből?

Sajnos a kézenfekvő válasz most sem a legjobb. Wald azt javasolta, hogy azokon a helyeken kell megerősíteni a páncélt, ahol a legkevesebb lyuk van. Ez elsőre talán furcsának tűnhet, azonban gondoljuk végig, Wald milyen repülőgépeket vizsgált. Pontosabban milyeneket nem: amelyek nem tértek vissza a bevetésről. Ha azt feltételezzük, hogy a lövedékek nagyjából egyenlő eséllyel találják el a repülőgép különböző pontjait, akkor teljesen logikus, hogy ahol kevesebb lyukat találunk, valójában azok a repülőgép gyenge pontjai. Hiszen azokat a gépeket, amelyeket ott ért találat, kisebb eséllyel tértek vissza. Ezért ezeket a részeket kell erős páncéllal megvédeni, hogy a lehető legtöbb emberéletet és drága repülőgépet óvjuk meg.

Milyen hibát nem követett el Wald? Nem feltételezte azt, hogy a gépek, amiket vizsgál az összes bevetésre indult gép véletlen mintáját alkotják. Tudta, hogy strukturálisan torzított a minta, amit vizsgál, hiszen csak a visszatérő gépeket látja. Ezt nevezzük túlélési torzításnak. Az egyszerű példa ezzel annyiban volt analóg, hogy mi is egy strukturálisan torzított mintát (a pozitív teszteredmények mintáját, ahol 67% a betegség valószínűsége) vizsgáltuk a teljes sokaságon belül. A teljes népesség körében 99%-os volt a teszt pontossága, azonban pozitív teszteredmények esetén a betegség valószínűsége már nagyban függ attól, hogy mennyire gyakori a betegség egyébként a teljes népességben. Fontos, hogy a minta, amit látunk a sokaságot milyen mértékben és feltevések mellett reprezentálja. Vagyis kell, hogy legyen valamilyen előzetes hitünk (ez hitnél sok esetben nem több!) a nagy eloszlásról, amit vizsgálunk. Ilyen hit az is, hogy csak a visszatérő gépeket látja Wald Ábrahám, de ez ebben az esetben tény.

A kérdés el is vezetett minket korunk két szembenálló statisztikai paradigmájához: a frekventista és a bayesiánus megközelítéshez. A bayes-i paradigma abban különbözik a frekventistától, hogy a sokaságról való információt (a visszatérő gépek csak a túlélők, a betegség a népesség 2%-ánál fordul elő) is felhasználja a becslése megalkotásához, így van arról elképzelése, hogy a minta, amit lát (a visszatérő gépek golyó ütötte lyukai, illetve a pozitív teszteredményünk) esetlegesen milyen torzítások mellett jöhetett ki a sokaságból. A frekventista ezzel szemben valamilyen sokaság torzítatlan, véletlen mintájaként értelmezi, amit lát. Az iskolában statisztika órán jellemzően ezt a megközelítést tanuljuk.

A frekventista megközelítést a gépeken golyó ütötte lyukak kapcsán akkor lehetne alkalmazni, ha véletlenszerűen vizsgálnánk lelőtt, és túlélő gépeket egyaránt. Az igazán érdekes azonban itt is az lenne, ha összehasonlítanánk a két különböző sorsú gépeket: miben különbözik a golyó ütötte lyukak mintázata a lelőtt, és a túlélő gépeken? A törzsen valószínűleg hasonló mennyiségű lyukat fogunk látni, viszont az üzemanyagtartálynál és a hajtóműnél csak a lelőtt gépeken lesznek sérülések. Persze ilyen vizsgálatot a valóságban ritkábban tudunk végezni.

A mindennapi életünk könnyed problémáihoz viszont általában sokat segíthet egy csipet bayes-i megközelítés. Például gondoljunk arra, hogy nem találjuk otthon a telefonunkat, ezért megcsörgetjük. Halljuk, hogy a csörgés a konyhából jön, hogyan álljunk neki a keresésnek? A frekventista egyszerűen a lehető legjobban megpróbálná meghatározni, honnan szól a csörgés, majd szisztematikusan átnézné annak környezetét. A bayesiánus ezzel szemben kombinálná a hallott hangot azzal az információval, hogy hova szokta rakni a telefonját, és ott kezdené a keresést, ami ezek alapján a legvalószínűbb hely. Ahova soha nem rakom a telefonom, ott valószínűleg most sem hagytam, még ha pillanatnyilag onnan is vélem hallani a csörgést.

A frekventista megközelítés uralkodása elsősorban egyszerűségének köszönhető. Kevesebb számítással, egzaktabb eredményeket kapunk általa: míg 2 frekventista mindig ugyanarra a következtetésre jut, ha helyesen dolgoznak, bayes-i vizsgálatok vezethetnek eltérő eredményre. Más feltételezésekkel indulhattak a sokaság eloszlására vonatkozóan! Ez pedig egy lényeges különbség: a frekventista vizsgálat végén kiderül, hogy a hipotézised igaz, vagy sem, míg a bayes-i vizsgálat oda vezet, hogy megerősíti, esetleg árnyalja előzetes hitünket.

A megfogalmazható tanács pedig az, hogy mindig vegyük figyelembe, hogy amit látunk, az egy mintája a sokaságnak, és a legtöbb esetben annak nem is véletlen mintája. Következtetéseket tehát ennek tudatában érdemes levonnunk. Általánosítani csak meglehetősen szigorú feltételek mellett lehetséges. Ennek tudatában biztosan kevesebbet tévedünk majd.