Van egy remek ötletem! Menjünk és kopasszuk meg jól a kaszinót! – Hangzott el már sokszor ez a mondat különböző baráti társaságok körében, egy-egy végig italozott éjszaka közepe felé. Nem is kell mondani, általában ezek a tervek kevésbé mondhatók sikeresnek, azonban néha mégis a mulatozók oldalára áll a szerencse. A következő cikkben azt fogjuk megvizsgálni, hogy miért érdemesebb kaszinót üzemeltetni, mint látogatni.

A kaszinó játékokról alapvetően érdemes tudni, hogy egy egyszerű pénzfeldobásnál valamennyivel bonyolultabbak, azonban nem kínálnak sokkal rosszabb valószínűséget a játékosoknak.  A legtöbb kaszinó játékban csupán pár százalékkal indul jobb helyzetből a ház, mint a kezdő vagy tapasztaltabb játékosok. A cikkben az egyszerűség kedvéért az egyik legnépszerűbb és mégis legegyszerűbb matematikával rendelkező játékot fogjuk vizsgálni, a rulettet.

A pénzfeldobás esetében a játékosnak és a háznak is 50-50% esélye van a nyerésre, és ha a kifizetés kétszeres, tehát megduplázhatjuk játékonként a tétünket, akkor látjuk azt, hogy ez egy nulla összegű játék, ami azt jelenti, hogy ha a végtelenségig játszanák akkor mind a két fél ugyanannyi pénzzel térne haza a nap végén, mint amennyivel elkezdték. A rulett és a többi kaszinó játék esetében, azonban ez nem így van.

Egy hagyományos európai stílusú rulett asztalon 37 db szám található, 0-tól 36-ig. A mezők szín szerinti eloszlásban 18 fekete, 18 piros és 1 zöld, a 0. A legegyszerűbb fogadási lehetőség az, ha egy mezőre helyezzük a tétünket és ha bejön, aminek az esélye 1/37 hiszen minden mezőre ugyanakkora eséllyel eshet a golyó, akkor a pénzünk 36-szorosát kapjuk vissza. Ebből látszik, hogy a játék itt már nem kiegyenlített, hiszen 36 egységet kapunk vissza, azonban várhatóan csak minden 37-edik gurításnál nyerünk, így hosszútávon, ha elég sokat játszunk, akkor a ház elviszi az összes pénzünket. Több fajta fogadási lehetőség is van az asztalnál, fogadhatunk például arra is, hogy a nyertes mező milyen színű lesz. Annak az esélye, hogy ezen nyerünk, azaz a tétünk kétszeresét kapjuk vissza, 18/37, azaz 48,6%. Ebből is látszik ,hogy a kaszinó haszna igazából nem tűnik nagynak, 2,7%, ami abból fakad, hogy az asztalon van egy zöld 0-s számjegy, ami egyik nagyobb kombinált fogadási lehetőségben ( színek, oszlopok, sorok) sincsen benne. Tehát, hogy ha 100 forintnyi tétet helyezünk egy mezőre , akkor várhatóan a gurítás során 2,7 forintot veszítünk. Természetesen nem 96,3 Ft-ot fogunk visszakapni, hanem a tétünk többszörösét a fogadás típusától függően vagy semmit. Ha ezt megnézzük 100 gurításra, akkor azt látjuk, hogy várhatóan elvesztünk 27 forintot.

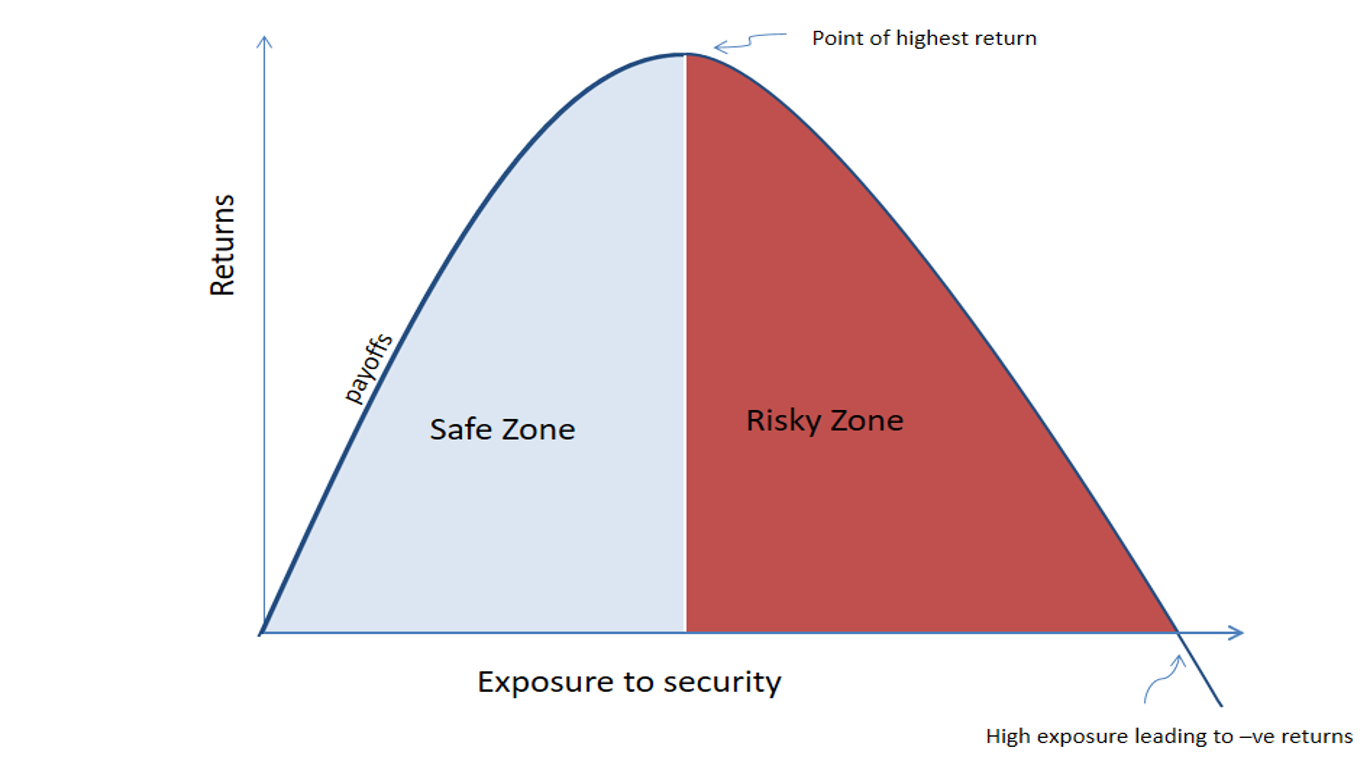
Ez a felállás igaz az összes kaszinókban játszott játékra, csak valamennyivel bonyolultabb matematikai háttérbe van öltöztetve a ház előnye.  Tegyük fel, hogy egy olyan világban élünk ahol a kaszinó játékok mind nulla-összegűek, tehát ha elég sokáig játszunk a ház ellen elég nagy tőkével, akkor várhatóan pénzünknél fogunk maradni vagy esetleg még a játékosok felé is dől a mérleg. Vajon egy ilyen világban is nyerne a kaszinó az átlagos játékosokkal szemben? A válasz erre a kérdésre sajnos az, hogy igen. Ugyanis a kaszinónak megvan az az előnnyel, hogy sokkal több zsetonnal rendelkezik, mint a vele szemben ülő egyéni játékosok. A válasz a tapasztalatlan kaszinó látogatók  gyakori vereségére egy a befektető és gyakorlott szerencsejátékosok között jól ismert fogalomban rejlik, ami nem más, mint a Kelly-kritérium. A Kelly-kritérium megmutatja azt, hogy adott kifizetések és valószínűségek mellett a pénzünk mekkora részét ajánlott feltenni tétként az elérhető hosszú távú maximális kifizetés érdekében.

Az f jelenti a pénzösszegünk azon hányadát, amit érdemes kockáztatni, a b jelenti azt a számot ahány szorosát nyerjük meg a feltett pénzünknek (egy hagyományos pénzfeldobás esetében b=1), a nyerés esélye p, q pedig a vereségé, tehát q=1-p.  Ha behelyettesítünk az egyenletbe, akkor megkapjuk, hogy 0 összegű játékok esetében nem érdemes kockáztatni a pénzünket. Ha egy ilyen játékot a végtelenségig játszanánk, akkor összességében se nem nyernénk se nem vesztenénk, de ez csak akkor lenne igaz, ha van elég tőkénk ahhoz, hogy kibírjuk hosszabb vesztő szériákat is. Azonban ha a nyerési esélyünk hirtelen 60%-ra ugrana, akkor elég tőkével vagyonokra tehétnénk szert, viszont a valóságban nem ezt látjuk.

Egy kísérlet során felmérték, hogy a játékosok ilyen feltételek mellett is többnyire veszítenek a házzal szemben, ugyanis a pénzük túlságosan nagy részét teszik fel tétnek és egy szerencsétlen sorozat esetén könnyen elfogy a tőkéjük. Azonban ha ismernék a Kelly-formulát akkor tudnák azt, hogy ilyen esetben csupán a pénzük 20%-át* érdemes egy dobásra feltenni és ezzel maximalizálni tudnák a várható nyereményüket. A formula természetesen nem csak szerencsejátékokra alkalmazható, hanem szinte mindenben mindenre, ahol kvantifikálható a várható kockázat ( tehát hogy mekkora eséllyel veszítjük el a befektetett pénzünket) és kifizetés mértéke. A formula olyan híres befektetők stratégiájában is megjelent mint John M. Keynes vagy Warren Buffet.

–––

További érdekességek a témában:

Száz János előadása

Leonardo Barichello – The last banana: A thought experiment in probability